Angles
Angles are one of the most basic and most used concepts in mathematics. They are used in physics, sports, art, construction… in almost every part of human activity, as well as in nature. They designate the measure of a rotation. It is almost impossible to go through life without encountering angles or having to use some knowledge about them. That is why we are going to show you a few basic things about them.
The easiest way to get a grasp around angles and the basic expressions that go with them is to imagine a clock. An analog clock, not a digital one. A clock that has hands and a dial and numbers from 1 to 12 marked on its face. Now, imagine that the clock shows that it is two o’clock in the afternoon, with the big hand on 12 and the little hand on two. In mathematical terms, those two hands represent rays that form an area which is called an angle. The center of the clock (the point in which the two hands meet) is called the vertex of the angle. The measure of an angle can be expressed using a number of units, but the most often used are radians and degrees.
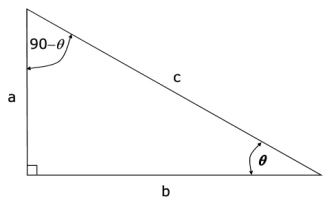
Radians are the ratios between the length of an arc and its radius. A degree is the 360th part of a full rotation. Again, if you are having trouble grasping that, remember the clock. As time passes, the hands of a clock move to a certain extent. If there was a pencil on the end of the big hand, every 60 minutes it would draw a full circle. In that case the hand made a 360 degree turn. Every minute, the measure of the angle between the position of the hand now and the position it held a minute before is 6 degrees (360/60). That is because it traveled the distance that is 1/60th of a full rotation. One degree is the angle the two positions form when the hand travels 1/6th of that distance.
Basic types of angles
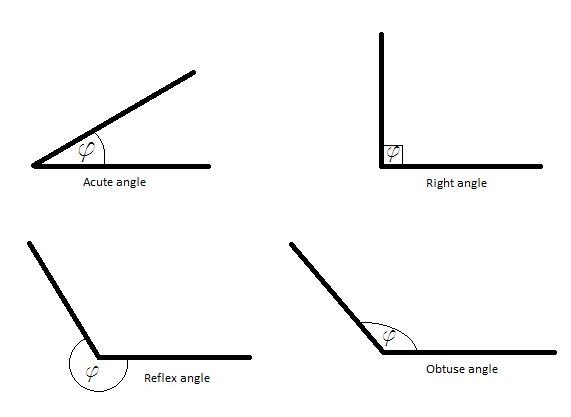
There are several basic types of angles, depending on their size. If they are smaller than ¼ of a rotation (or 90 degrees) are called acute angles. If the measure of an angle is exactly 90 degrees, it is called a right angle. If the measure of an angle is larger than 90 degrees, but smaller than 180 degrees, the angle is called an obtuse angle. The one that is precisely 180 degrees large is called a straight angle (basically, this one is a straight line – think of a clock showing 9.15 am). An angle that is larger than 180 degrees but smaller than a full turn is called a reflex angle.
Relationships between angles
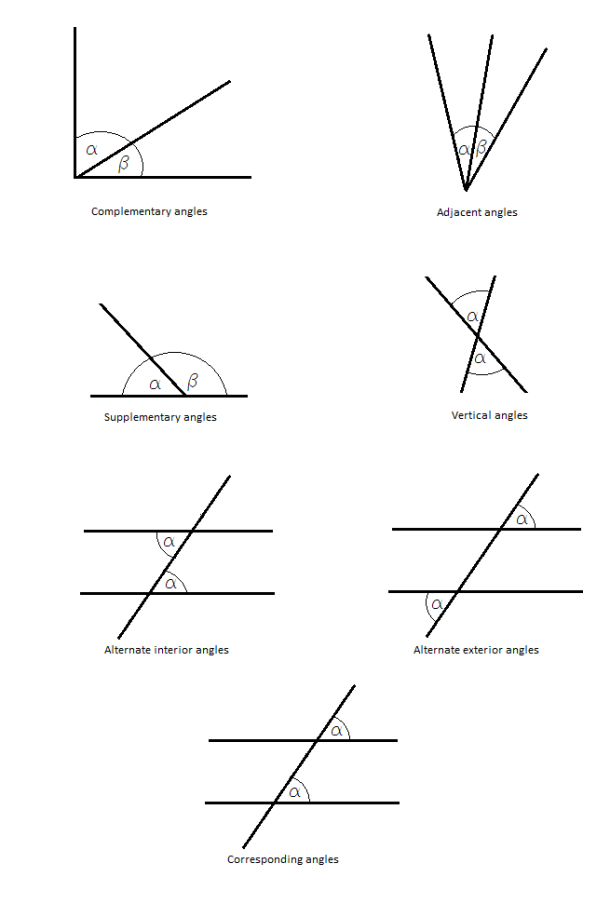
Adjacent angles are two angles that are side by side and share a common ray. Complementary angles are the angles that add up to 90 degrees. Supplementary angles are two angles that add up to 180 degrees. When two rays intersect, they form four angles. The angles that directly oppose each other in that setup are called vertical angles.
These are the bare basics you have to know when it comes to angles. As we proceed to collect more mathematical knowledge, this article will be expanded to provide the information about angles necessary for understanding the more complex subjects.
If you wish to practice what you learned about angles so far, please feel free to use the math worksheets below.
Angles exams for teachers
Plane figures – angle relationships worksheets for students
| Worksheet Name | File Size | Downloads | Upload date |
| Plane Figures – Angles – Draw an angle | 931.1 kB | 2901 | September 3, 2019 |
| Plane Figures – Angles – Measure an angle | 1 MB | 3139 | September 3, 2019 |
| Angle Relationships – Name the relationship | 6.8 MB | 3988 | September 3, 2019 |
| Angle Relationships – Find angle measures | 7.5 MB | 6314 | September 3, 2019 |
| Angle Relationships – Solve equations | 9 MB | 33296 | September 3, 2019 |