Squares and square roots
Squares and square roots are basic mathematical terms that you will encounter very often, especially in functions and different equations. They are easy to understand and once you figure them out, a new door into the world of exponents and more complex mathematics will open for you.
Squares
Squares or perfect squares (as they are sometimes called) are the result of numbers multiplied with themselves. So for example, the square of number 3 would be number 9 because 3 times 3 is 9. For the same reason, the square of number 4 would be 16, for number 5 it would be 25 and so on. We will illustrate this to make it a bit clearer.
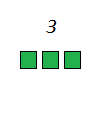
Here we have 3 small squares. If we take two more rows like that, we can arrange them in a perfect square. That big square consists of 9 small squares. In fact, a number is considered a square number only if you can arrange that number of points in a square. Like this:
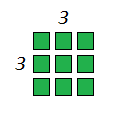
There are a couple of important things to remember. The square root of 1 is 1 (no surprise there because 1*1=1). A square always has a positive value (because a negative number multiplied with a negative number always gives a positive result). The usual notation for the square of a number (represented here with the variable x) is x2.
Also, a handy bit of information is that the square of an even number is also an even number (generic cialis online). It is also divisible by four. No exceptions. And the square of an odd number is always an odd number.
Square roots
Square roots are the inverse functions of squares. A square root of a number is the number you multiplied with itself to get the number whose square you are looking for. Sounds complicated? Let me rephrase that. If we had a square with an area of A, the square root of A would be the length of one side of that square. That means that, the square root of number 36 would be 6. But also, the square root of number 36 is (-6). It is important to remember that every positive real number has two square roots – one positive and one negative.
Since there are no negative square numbers, real square roots of negative numbers do not exist. In fact, the square root of -1 (and all other negative numbers) is called an imaginary number (i). But we will get to them a bit later, after we post the lessons necessary for understanding them. For now – take our word for it.
The unique, non negative square root of every real number is called the principal square root. The term whose root we are interested in is called the radicand.
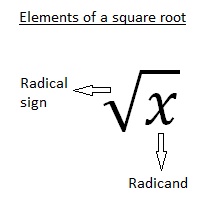
These are the basic things about squares and square roots. If you wish to practice what you learned about square roots, please feel free to use the mathematical worksheets below.
Square roots exams for teachers
| Exam Name | File Size | Downloads | Upload date |
|
Integers
|
|||
| Square Roots – Integers – very easy | 555.9 kB | 11983 | September 3, 2019 |
| Square Roots – Integers – easy | 556.1 kB | 9241 | September 3, 2019 |
| Square Roots – Integers – medium | 557.1 kB | 13161 | September 3, 2019 |
| Square Roots – Integers – hard | 556.1 kB | 9344 | September 3, 2019 |
|
Decimals
|
|||
| Square Roots – Decimals – very easy | 561.2 kB | 3377 | September 3, 2019 |
| Square Roots – Decimals – easy | 562.5 kB | 3235 | September 3, 2019 |
| Square Roots – Decimals – medium | 563.3 kB | 4218 | September 3, 2019 |
| Square Roots – Decimals – hard | 564 kB | 2692 | September 3, 2019 |
| Square Roots – Decimals – very hard | 566 kB | 3413 | September 3, 2019 |
|
Fractions
|
|||
| Square Roots – Fractions – very easy | 577 kB | 3651 | September 3, 2019 |
| Square Roots – Fractions – easy | 578 kB | 3311 | September 3, 2019 |
| Square Roots – Fractions – medium | 577.4 kB | 4012 | September 3, 2019 |
| Square Roots – Fractions – hard | 580 kB | 3300 | September 3, 2019 |
| Square Roots – Fractions – very hard | 584 kB | 3362 | September 3, 2019 |
Square roots worksheets for teachers
| Worksheet Name | File Size | Downloads | Upload date |
| Square Roots – Integers | 2.8 MB | 10543 | September 3, 2019 |
| Square Roots – Decimals | 3.2 MB | 3716 | September 3, 2019 |
| Square Roots – Fractions | 4.1 MB | 5705 | September 3, 2019 |