The distance formula
The distance formula helps you calculate how far apart two points in a coordinate system are. To do this, it uses the Pythagorean theorem and its properties. Like this:
Draw a point in two dimensional Cartesian space. Now draw a line connecting that point with the point of origin. Do you see it? If not, draw a line passing through the point you selected that is perpendicular to the horizontal x-axis. You should notice that the line you just drew, together with the part of the x-axis and the line connecting your point to the point of origin, forms a right triangle. The line that connects your point and O is the hypotenuse of said triangle and the other two lines are the legs.
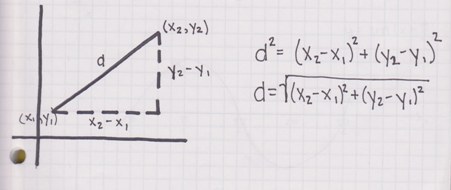
Now, you probably remember the Pythagorean theorem from the last lesson. If not, click on the Pythagorean theorem and refresh your memory. If you do, you probably remember that the length of the hypotenuse in a right triangle can be calculated using the formula:
c2 = a2 + b2
This is the basis of the distance formula. The square of the length of the hypotenuse is the sum of squares of the lengths of both legs. The length of a leg of the triangle in a coordinate system is the distance between two points in space that are the endpoints of that particular line. For clarity, let us call the line along the x-axis side a, and the line parallel to the y axis side b. Since none of the points that make side a do not change their position in relation to the y axis, the distance between them is simply the difference in size of the x-coordinates of the endpoints. Like this:
a = x2 – x1
And that is the length of side a. The length of side b can be calculated in much the same way, only the coordinate that remains fixed is the x-coordinate (instead of the y-coordinate, as it was with side a). That means that the length of side b is:
b = y2 – y1
Now since we know both legs, we can insert these small expressions in our equation and get:
C2 = (x2 – x1)2 + (y2 – y1)2
If you calculate the square root of this equation, you will get what is called the distance formula.
The distance formula can be applied to calculate the distance between any two points in Euclidean space and it will be very useful in many occasions.
If you wish to practice what you learned about the distance formula, please feel free to use the math worksheets below.
The distance formula exams for teachers
| Exam Name | File Size | Downloads | Upload date |
|
Integers
|
|||
| The distance formula – Integers – easy | 203.7 kB | 6920 | September 3, 2019 |
| The distance formula – Integers – medium | 206 kB | 6226 | September 3, 2019 |
| The distance formula – Integers – hard | 238 kB | 4008 | September 3, 2019 |
| The distance formula – Integers – very hard | 279.4 kB | 3262 | September 3, 2019 |
|
Decimals
|
|||
| The distance formula – Decimals – easy | 276.2 kB | 2256 | September 3, 2019 |
| The distance formula – Decimals – medium | 284.3 kB | 2402 | September 3, 2019 |
| The distance formula – Decimals – hard | 292 kB | 2449 | September 3, 2019 |
| The distance formula – Decimals – very hard | 306.7 kB | 1974 | September 3, 2019 |
|
Fractions
|
|||
| The distance formula – Fractions – easy | 773.4 kB | 2297 | September 3, 2019 |
| The distance formula – Fractions – medium | 797.5 kB | 2343 | September 3, 2019 |
| The distance formula – Fractions – hard | 800.8 kB | 2214 | September 3, 2019 |
The distance formula worksheets for students
| Worksheet Name | File Size | Downloads | Upload date |
| The distance formula – Integers | 2.9 MB | 7091 | September 3, 2019 |
| The distance formula – Decimals | 541 kB | 3250 | September 3, 2019 |
| The distance formula – Fractions | 3.6 MB | 2413 | September 3, 2019 |
| The distance formula – Integers – Line segment | 12.8 MB | 4241 | September 3, 2019 |