Inequalities
Inequalities are a way to express the relative size of two numbers or objects, that being that one of those objects is smaller, greater or equal in size in relation to the other object. You can express inequalities graphically via a number line or as a mathematical expression. A number line is a straight line on which every point represents a single real number and it is very easy to portrait inequalities on it. For example, let us say you get an expression that says:
X is greater than 9.
The solutions of this problem (or the value of X) are values on the number line that are greater than 9 and you should mark these values. Be careful not to mark the number 9 as well, because the assignment asks only for the values greater than that number. Now, let us say that the assignment states that:
X is greater than or equal to 9
In this case the solution would include the number 9 because it is permitted in the text of the assignment that x can be equal to 9.
Inequalities also come in forms of longer mathematical expressions, similar to equations. Depending on the number of steps you have to perform in order to solve them, they can also be divided into one-step inequalities, two-step inequalities or multi-step inequalities.
Inequalities can be in five different ways and each of them represents different relations between the objects that are being compared (levitra online). We are going to explain them to you in this table using both mathematical symbols and text.
|
Symbols |
Meaning |
|
a < b |
The value of a is less than the value of b |
|
a > b |
The value of a is greater than the value of b |
|
a ≠ b |
The value of a is not equal to the value of b |
|
a ≤ b |
The value of a is less than or equal to the value of b |
|
a ≥ b |
The value of a is greater than or equal to the value of b |
The expression for the value of a being not equal to the value of b can also be expressed with the symbol “<>” instead of the symbol “≠”, but they mean the same. In this case, a can be any number on the number line except b.
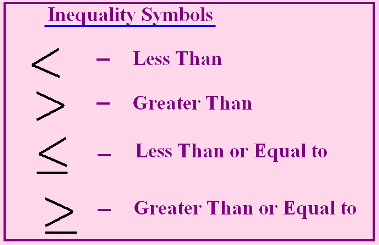
Properties of inequalities
Inequalities have five basic properties: transitivity, addition and subtraction, multiplication and division, additive inverse and finally, multiplicative inverse.
The property of transitivity states that for a, b, and c being any real numbers:
|
If |
a < b and b > c |
then |
a > c |
|
If |
a > b and b < c |
then |
a < c |
|
If |
a ≤ b and b = c |
then |
a > c |
|
If |
a ≥ b and b = c |
then |
a < c |
The rules that deal with the properties of addition and subtraction within inequalities say that for a, b and c being any real numbers:
|
If |
a < b |
then |
a + c < b + c |
and |
a – c < b – c |
|
If |
a > b |
then |
a + c > b + c |
and |
a – c > b – c |
The rules that deal with the properties of multiplication and division within inequalities state that for a, b and c being any real numbers:
|
If |
c positive and a < b |
then |
ac < bc |
and |
a/c < b/c |
|
If |
c negative and a < b |
then |
ac > bc |
and |
a/c > b/c |
The property of the additive inverse says that for a and b being any real numbers:
|
If |
a < b |
then |
– a > – b |
|
If |
a > b |
then |
– a < – b |
The property of the multiplicative inverse states has two parts. If a and b are both positive or both negative real numbers, then:
|
If |
a < b |
then |
1/a > 1/b |
|
If |
a > b |
then |
1/a < 1/b |
If either a or b is negative, then:
|
If |
a < b |
then |
1/a < 1/b |
|
If |
a > b |
then |
1/a > 1/b |
If you wish to practice with inequalities, check the free worksheets below.
Inequalities exams for teachers
| Exam Name | File Size | Downloads | Upload date |
|
Integers
|
|||
| Graph inequalities – Integers – easy | 245.3 kB | 8111 | September 3, 2019 |
| Graph inequalities – Integers – medium | 234.6 kB | 10922 | September 3, 2019 |
| Graph inequalities – Integers – hard | 238.7 kB | 5030 | September 3, 2019 |
|
Decimals
|
|||
| Graph inequalities – Decimals – easy | 223.2 kB | 3343 | September 3, 2019 |
| Graph inequalities – Decimals – medium | 221 kB | 3400 | September 3, 2019 |
| Graph inequalities – Decimals – hard | 224.6 kB | 3304 | September 3, 2019 |
|
Fractions
|
|||
| Graph inequalities – Fractions – easy | 232.4 kB | 2731 | September 3, 2019 |
| Graph inequalities – Fractions – medium | 243.1 kB | 2667 | September 3, 2019 |
| Graph inequalities – Fractions – hard | 270 kB | 2465 | September 3, 2019 |
Inequalities worksheets for students
| Worksheet Name | File Size | Downloads | Upload date |
| Graph inequalities – Integers | 2.4 MB | 6677 | September 3, 2019 |
| Graph inequalities – Decimals | 2.2 MB | 3311 | September 3, 2019 |
| Graph inequalities – Fractions | 746.5 kB | 3378 | September 3, 2019 |
| Inequality for given graph | 527.1 kB | 4660 | September 3, 2019 |