Numbers

Numbers are mathematical objects used to represent quantities. In other words, they are used to count and measure. They also make the foundation of all mathematics since they are probably the first mathematical concept ever created.

Numbers are visually represented by symbols called numerals. Numerals we widely use today (such as 1, 2, 3, 8, 21) are called Hindu-Arabic numerals. They were introduced in Europe probably in the 12^th century by an Italian mathematician called Leonardo Pisano, better known as Fibonacci  – one of the most important mathematicians of his age, who was educated in them during his time in North Africa.

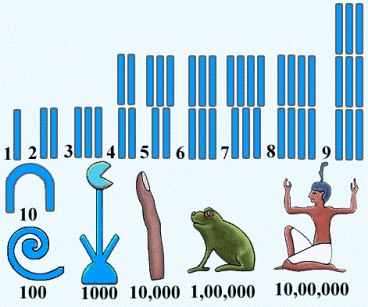
Before the Hindu-Arabic system was accepted as an international standard, there was a number of systems of numerals in use. For example, the most basic systems in which the number of objects counted is represented by the corresponding number of symbols are called unary systems. These systems are only useful for representing small, natural numbers as they become very impractical when large numbers are needed. This fact led to the invention of systems which use different symbols to abbreviate the unary notation.

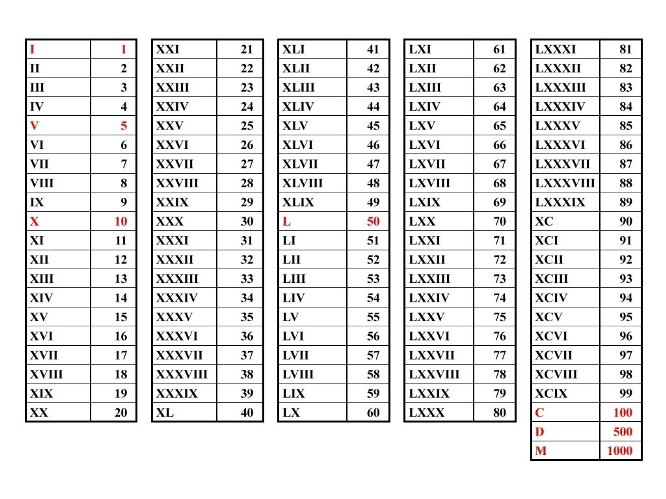
The best known of these systems were the system of Roman numerals and the Egyptian number system. They were later replaced by the systems which use abbreviations for repetitions of symbols (e.g. Chinese numerals) and finally the positional system in use today.

Depending on their type, numbers can be classified into sets or number systems. Numbers belonging to most basic number systems are called natural numbers (0, 1, 9, 24, 365 and so on). If we expand this system by introducing negative numbers (-1, -5, -28…) we get a set of numbers called integers. Fractions belong to the system of rational numbers, while real numbers are expressed using decimals. A number belonging to the complex number system is made of two components: a real number and the symbol i which represents the square root of -1.

Numbers can be used to express any kind of quantitative information. They can also be combined and changed through the use of mathematical operations. The basic mathematical operations are counting, addition and subtraction, multiplication and division. From them, a whole array of more complex mathematical operations arose, which provided us with the tools to describe the laws of nature.

This section is dedicated to numbers, their variations and to the different sets of numbers.

Numbers Categories