Circle
A circle is a plane figure, a shape in Euclidian geometry that consists of points which are all equally distant from a given point in space. That distance is called the radius (r) and that given point is called the center (marked by the symbol O ). A straight line that connects two points on the opposite sides of a circle and goes through the center is called the diameter (d). Its length is twice the length of the radius.
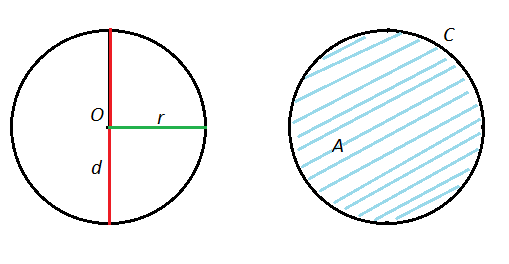
Circumference of a circle
The circumference of a circle (we will use the letter C as the symbol) is the length of the curved line that forms the circle or, in other words, the distance around the outside of the circle. It can be calculated using the formula:
C = 2 * r * π
or
C = d * π
Let us go and find the circumference of this circle as an example:
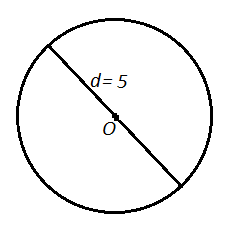
Its diameter is 5 cm, so when we introduce that measure into the formula, we get:
C = 5π cm
You can leave the result in this form, it is perfectly fine. In fact, this is considered an exact result. But if you wish to (for whatever reason) convert it into numbers, just do the multiplication and round the result to the nearest tenth or any number of decimals you want.
Area of a circle
The Greek mathematician Archimedes determined that the area a circle encloses (A) is equal to the area enclosed by a triangle whose base is the same length as the circumference of the circle and whose height is equal to the radius of the circle. The formula that we use to calculate that area is:
A = π * r2
As an example, we will now find the area of this circle:
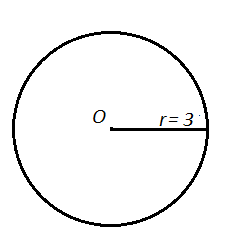
You can see that the radius of this circle is 3 cm. We put that number into our formula and we get:
A = π * 32
A = 9π cm
As before, you can opt to leave the result as it is or do the multiplication and get a completely numeric result.
More examples
Calculate the area of a circle whose circumference is 8π centimeters in length.
This example is a bit more complicated since it requires some thinking and a bit more calculation, but it is very simple to solve. First, we will write down the formula for the circumference and insert the values we know. This will allow us to calculate the radius of the circle.
C = 2 * r * π
8π = 2 * r * π |: 2π
r = 4 cm
Now that we know the radius, we just have to insert it into the area formula and do the simple math.
A = π * r2
A = π * 42
A = 16π cm2
Our solution is 16π cm2, or if we push it a bit further:
A = 50,3 cm2
These are the basic mathematical terms and concepts connected to circles. As we expand the base of knowledge here on MathX, we will add new information to this article as well. If you wish to practice what you learned about the circle so far, please feel free to use the math worksheets below.
Circle exams for teachers
| Exam Name | File Size | Downloads | Upload date |
|
Radius
|
|||
| Circles – Radius – very easy | 257.1 kB | 2678 | September 3, 2019 |
| Circles – Radius – easy | 264.6 kB | 2448 | September 3, 2019 |
| Circles – Radius – medium | 528.8 kB | 2946 | September 3, 2019 |
| Circles – Radius – hard | 532.5 kB | 2634 | September 3, 2019 |
| Circles – Radius – very hard | 285.5 kB | 2666 | September 3, 2019 |
|
Diameter
|
|||
| Circles – Diameter – very easy | 221.4 kB | 2509 | September 3, 2019 |
| Circles – Diameter – easy | 288 kB | 2267 | September 3, 2019 |
| Circles – Diameter – medium | 538.7 kB | 2647 | September 3, 2019 |
| Circles – Diameter – hard | 537.6 kB | 2469 | September 3, 2019 |
| Circles – Diameter – very hard | 532 kB | 2474 | September 3, 2019 |
|
Circumference
|
|||
| Circles – Circumference – very easy | 221.4 kB | 2509 | September 3, 2019 |
| Circles – Circumference – easy | 288 kB | 2267 | September 3, 2019 |
| Circles – Circumference – medium | 535.9 kB | 2836 | September 3, 2019 |
| Circles – Circumference – hard | 534.6 kB | 2451 | September 3, 2019 |
| Circles – Circumference – very hard | 535.5 kB | 2682 | September 3, 2019 |
|
Area
|
|||
| Circles – Area – very easy | 283 kB | 2453 | September 3, 2019 |
| Circles – Area – easy | 278.8 kB | 2559 | September 3, 2019 |
| Circles – Area – medium | 538.5 kB | 2825 | September 3, 2019 |
| Circles – Area – hard | 539.4 kB | 2432 | September 3, 2019 |
| Circles – Area – very hard | 545.4 kB | 2578 | September 3, 2019 |
|
Complete
|
|||
| Circles – Complete – very easy | 267.1 kB | 2659 | September 3, 2019 |
| Circles – Complete – easy | 281.7 kB | 2478 | September 3, 2019 |
| Circles – Complete – medium | 538.5 kB | 2825 | September 3, 2019 |
| Circles – Complete – hard | 539.4 kB | 2432 | September 3, 2019 |
| Circles – Complete – very hard | 545.4 kB | 2578 | September 3, 2019 |
Circle worksheets for students
| Worksheet Name | File Size | Downloads | Upload date |
| Circles – Radius | 8 MB | 2787 | September 3, 2019 |
| Circles – Diameter | 8.4 MB | 2756 | September 3, 2019 |
| Circles – Circumference | 45.9 kB | 7321 | September 3, 2019 |
| Circles – Area | 45.1 kB | 3442 | September 3, 2019 |