Proportions and Similarity
Proportions in mathematics can be viewed from a few perspectives. For instance, the proportionality of two variable values is determined by checking if one of the values is the product of the other value and some constant. In other words, two variable values (numbers or quantities) are proportional if their ratio is a constant, called the coefficient of proportionality or the proportionality constant. This is best explained using the linear equation:
y = k*x
If k is a constant quantity, x will always be proportional to y for every possible value. Then k is considered to be the coefficient of proportionality.
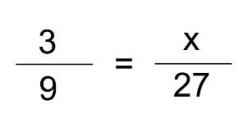
Proportion is also the name we use when describing the equality of two ratios. If the ratios in question are equal, we say that they are proportional. For example, we have two ratios here:
5/6 = 15/18
These ratios are proportional because when we multiply both the numerator and the denominator of the ratio 5/6 by 3, we get 15/18 as a result. That is also true for the other way around – if we simplify the second ratio by dividing its numerator and denominator by 3, we get the first ratio as a result. Let us try another example:
2/3 = 8/9
As you can see, this equation is not valid – 8 is the product of 2 times 4 and 9 is the product of 3 times 3. That means that these ratios are not proportional. If we wanted to find the proportional ratio to 2/3 while keeping the denominator of the other ratio, we would have to multiply the numerator 2 with the number 3. So the correct proportion would be:
2/3 = 8/9
Similarity is a form of proportion used to compare sizes of shapes and objects and the same rules apply when solving both similarity and proportion. Knowing your way around similarities is especially useful when working with maps, blueprints and models. In those cases you are often given a ratio. The ratio of 1 : 3 in a model means that 1 cm on the model represents 3 cm on the actual object. The important thing to remember is that for two shapes or objects to be similar, they have to have the same shape and all of their sides have to be proportional (cialis online). That means that if one side of an object has been reduced by a factor of 2, all other sides have to be reduced by the same factor if they are to be similar. Let us try to solve a word problem with similarity.
A map has a scale of 1 cm : 20 km. If Elm Grove and Small Creek are 100 km apart, then they are how far apart on the map?
The first thing we should do is to form a proportion. Since the distance between Elm Grove and Small Creek on the map is unknown, it would look like this:
1/20 = x/100
Now, we just have to get rid of the second denominator to find the value of x. We will do it by multiplying the whole equation by 100:
1/20 = x/100 |*100
100/20 = x
x = 5
Now we know that the distance between Elm Grove and Small Creek on the map is 5 cm.
This approach can be used on various similar examples. If you wish to practice proportions and similarity, feel free to use the worksheets below.
Proportions exams for teachers
| Worksheet Name | File Size | Downloads | Upload date |
|
Check valid proportion
|
|||
| Checking for proportion – easy | 459.5 kB | 6360 | September 3, 2019 |
| Checking for proportion – medium | 459.4 kB | 6147 | September 3, 2019 |
| Checking for proportion – hard | 459.6 kB | 4936 | September 3, 2019 |
|
Solve proportions
|
|||
| Solving proportions – Integers to fractions – easy | 461.8 kB | 5805 | September 3, 2019 |
| Solving proportions – Integers to fractions – medium | 462.2 kB | 5415 | September 3, 2019 |
| Solving proportions – Integers to fractions – hard | 462.2 kB | 3973 | September 3, 2019 |
| Solving proportions – Integers to decimals – easy | 461.2 kB | 2701 | September 3, 2019 |
| Solving proportions – Integers to decimals – medium | 461.6 kB | 2601 | September 3, 2019 |
| Solving proportions – Integers to decimals – hard | 465.2 kB | 3087 | September 3, 2019 |
| Solving proportions – Decimals to decimals – easy | 461.4 kB | 2416 | September 3, 2019 |
| Solving proportions – Decimals to decimals – medium | 11.3 kB | 2324 | September 3, 2019 |
| Solving proportions – Decimals to decimals – hard | 461.8 kB | 2589 | September 3, 2019 |
|
Word problems
|
|||
| Proportions – Word problems – easy | 458.9 kB | 7991 | September 3, 2019 |
| Proportions – Word problems – medium | 460.4 kB | 7827 | September 3, 2019 |
| Proportions – Word problems – hard | 460.5 kB | 10331 | September 3, 2019 |
|
Similar proportions
|
|||
| Similar figures – very easy | 631.1 kB | 6586 | September 3, 2019 |
| Similar figures – easy | 651.4 kB | 8133 | September 3, 2019 |
| Similar figures – medium | 710.3 kB | 13200 | September 3, 2019 |
| Similar figures – hard | 722.1 kB | 8148 | September 3, 2019 |
| Similar figures – very hard | 705.7 kB | 6001 | September 3, 2019 |
|
Similar proportions – Word problems
|
|||
| Similar figures – Word problems – easy | 459.3 kB | 8995 | September 3, 2019 |
| Similar figures – Word problems – medium | 459.7 kB | 17495 | September 3, 2019 |
| Similar figures – Word problems – hard | 460.4 kB | 6946 | September 3, 2019 |
Proportions worksheets for students
| Worksheet Name | File Size | Downloads | Upload date |
| Checking for a proportion | 532.1 kB | 4083 | September 3, 2019 |
| Solving proportions of integers | 566.6 kB | 4690 | September 3, 2019 |
| Solving proportions of decimals | 566.8 kB | 2444 | September 3, 2019 |
| Proportions – Word problems | 557.4 kB | 11323 | September 3, 2019 |
| Proportions – Similar figures – Integers | 3 MB | 7408 | September 3, 2019 |
| Proportions – Similar figures – Decimals | 545.2 kB | 4754 | September 3, 2019 |
| Proportions – Similar figures – Word problems | 552.2 kB | 13349 | September 3, 2019 |