Quadrilaterals
Quadrilaterals are plane figures (polygons) that have four sides (called edges) and four angles (corners or vertices). They are sometimes also called quadrangles or tetragons. Broadly, they can be divided into three types known as topological types. These types are: convex, concave and crossed quadrilaterals.
Convex and concave quadrangles are also considered simple quadrilaterals and as such the sum of their interior angles adds up to 360 degrees. This is a very useful piece of information as you are going to use it very often when calculating missing angles and the procedure is basically the same as it is with triangles.
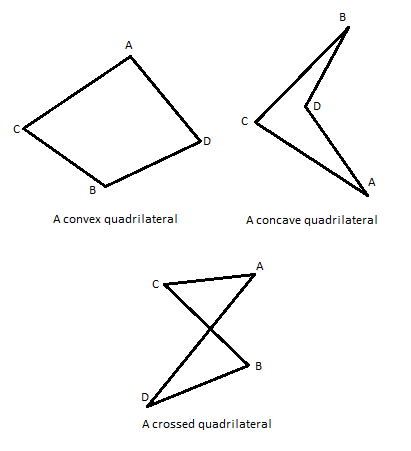
Types of quadrilaterals
There are several different types of convex quadrilaterals. These are the ones you will encounter most often:
– Rhombus – all of its sides are the same length. It is often called a diamond or a lozenge, although the latter name refers to a specific rhombus that has a 45 degree angle.
– Rhomboid – the length of its adjacent sides is unequal and its angles are oblique.
– Rectangle – a quadrangle with four right angles.
– Square – a rectangle with four equal sides.
– Oblong – a non-square rectangle. In other words, every rectangle with unequal adjacent sides is considered an oblong.
– Trapezoid – called trapezium in the UK, it is a convex tetragon with one pair of parallel sides.
– Isosceles trapezoid – a special type of trapezoid. Its base angles have the same measure and the other pair of opposite sides is the same length.
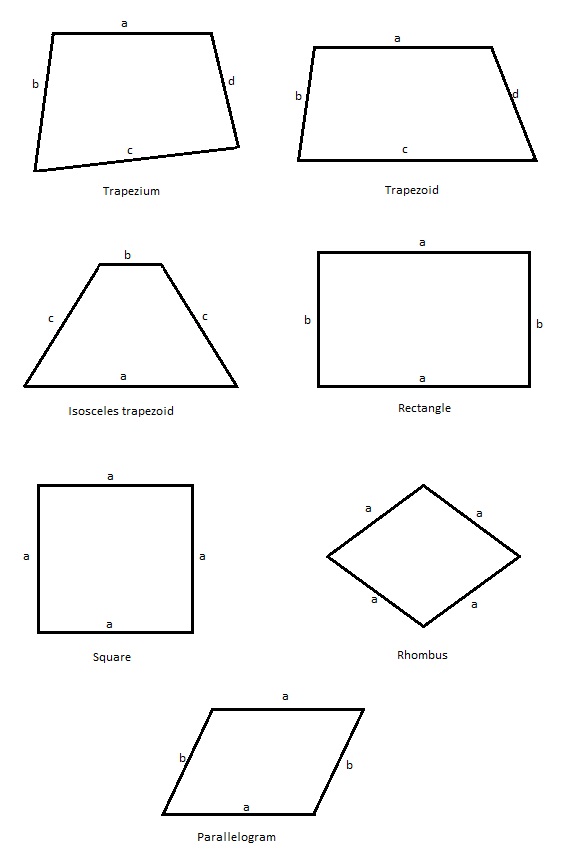
The square, rectangle, rhombus and rhomboid are considered parallelograms – tetragons with two pairs of parallel sides.
Finding the area of quadrilaterals
As it is with most plane figures, the area of some quadrilaterals is easier to calculate than other.
Quadrilaterals that demand the least amount of effort in order to calculate their areas are squares. The only thing you have to do to find the area of a square is to multiply the length of one of its sides with itself (does not matter which one – they are all the same length).
The second easiest quadrilateral to work with is the rectangle. Its area can be calculated by simply multiplying the length of side a (which is one length) with the length of side b (which is a different length). Since there are two pairs of sides with the same length in a rectangle, this is a very simple task.
The procedure for calculating the area of other quadrilaterals will be explained via examples.
Example 1:
Calculate the area of a parallelogram (K) whose height is 90mm and whose base is 9 cm long.
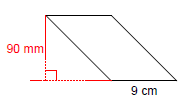
Again, this is easier than it looks. Because a parallelogram consists of two pairs of equally long parallel sides, its area can be calculated using the same formula that is used in calculating the area of a rectangle. The only difference is that instead of multiplying two sides of the quadrilateral, we multiply the length of its base with its height (remember the triangle). The one thing you should be mindful of is the use of the units of measurement. Make sure they are consistent. If they are not, convert them to the most convenient unit. So, in this case we get:
K = b * h
K = 9 * 9
K = 81 cm2
We can now see that the area of that particular parallelogram is 81 cm2. We converted 90 mm into 9 cm (1cm equals 10mm) for the purpose of consistency and convenience (smaller numbers).
Now, let us solve another example.
Example 2:
Calculate the area of this trapezoid. Its height is 980 cm, the smaller base (a) is 440 cm long and the length of its larger base (b) is 13.8 m.
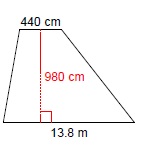
First, let us convert the centimeters into meters for easier calculation. Since one meter equals 100 cm, the height of the trapezoid is 9.8 m and the length of the smaller base is 4.4 meters.
Now, we have to find a way to calculate the area of this trapezoid. It consists of one rectangle and two (in this case –different) triangles. You will maybe see it better if we rearrange it a bit to look like this:
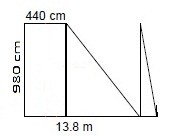
Now you see that this trapezoid consists of a rectangle whose sides are 4.4 and 9.8 meters long and two triangles whose measures we do not fully know yet (sildenafil online). But if you look at them closely, you will notice that you can encase them in a rectangle whose sides are 9.4 (we subtract the length of the shorter base from the length of the longer base) and 9.8 meters (the height). Since these two triangles are right triangles, their combined area is half the area of the rectangle we mentally drew around them. So, the size of the area of this trapezoid would be:
K = ((a + b) / 2) * h
K = ((4.4 + 13.8) / 2) * 9.8
K = (18.2 / 2) * 9.8
K = 9.1 * 9.8
K = 89.18 m2
This is the basic information you need to wrap your head around these very common plane figures. If you wish to practice what you learned about quadrilaterals, please feel free to use the math worksheets below.
Quadrilaterals exams for teachers
Quadrilaterals worksheets for students
| Worksheet Name | File Size | Downloads | Upload date |
| Quadrilaterals – Identify | 3.2 MB | 4031 | September 3, 2019 |
| Quadrilaterals – Find the missing angle measure | 2.9 MB | 5368 | September 3, 2019 |
| Quadrilaterals – Solve the equation | 551.6 kB | 4060 | September 3, 2019 |
| Quadrilaterals – Squares area | 4.1 MB | 2595 | September 3, 2019 |
| Quadrilaterals – Rectangles area | 3.8 MB | 2870 | September 3, 2019 |
| Quadrilaterals – Parallelograms area | 4.8 MB | 3211 | September 3, 2019 |