Triangles
Triangles are plane figures (or polygons) that have only three sides (edges) and three corners (vertices). Along with circles and quadrilaterals (four-sided polygons), they are the most basic of all plane figures. Also, their properties make them one of the most applicable geometric shapes in science and engineering.
There are several basic facts about them you should be aware of. The first fact is that the sum of the measures of all internal angles inside any triangle is exactly 180 degrees. This means that if you know the measure of two angles inside a triangle, you can easily determine the measure of the third one by subtracting the combined size of the two known angles from 180 degrees.
Secondly, a triangle also has something called exterior angles. Exterior angles are supplementary to their corresponding interior angles and the sum of their measures is always 360 degrees. Also, if you know the measure of an exterior angle, you can calculate the measure of its corresponding interior angle by subtracting the measure of the known angle from 180 degrees.
The third fact to keep in mind is that the sum of the lengths of any two sides of a triangle is larger than the length of the third side and that is a rule with no exceptions. This fact is also known as the principle of triangle inequality.
The fourth fact to remember (and it is a very important one) is that two triangles can be similar. They are similar if at least two angles in a triangle are the same as the corresponding angles in the other triangle. Also, they are similar if two or three of their corresponding sides are proportional. If the two triangles are the same in size and shape, they are considered congruent.
Types of triangles
We can classify a triangle according to two criteria: by its relative lengths of sides and by its internal angles.
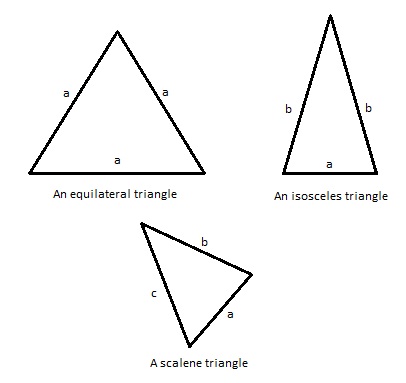
By the relative lengths of its sides, a triangle can be:
– An equilateral triangle – all of its sides are the same length and the measure of its interior angles is the same (60 degrees each).
– An isosceles triangle – two of its sides are equal, as well as their corresponding angles.
– A scalene triangle – all of its sides are unequal. Its angles are also different in measure.
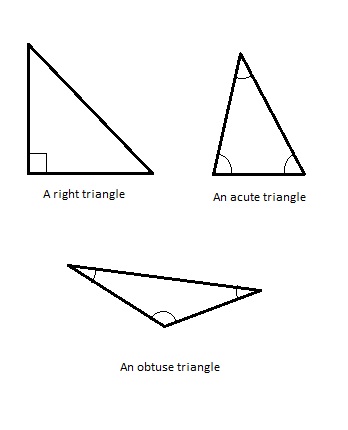
By internal angles, a triangle can be:
– A right triangle – also called a right-angled or a rectangle triangle is the one that has one of its interior angles measuring 90 degrees. They obey the Pythagorean theorem and have special names for their sides. The side opposite to the right angle is called the hypothenuse and it is the longest side of the triangle. The other two sides are legs or catheti of the triangle.
– An oblique triangle – the one in which no angles measure 90 degrees.
– An acute triangle – a triangle in which the measures of all angels are smaller than 90 degrees.
– An obtuse triangle – the triangle in which one of the angles is larger than 90 degrees.
Area of a triangle
There are a couple of ways to calculate the area of a triangle (T). The simplest formula is:
T = (b * h)/2
The letter b is the symbol for the length of the base of the triangle and the letter h we use to mark the height (altitude) of the triangle. This is the formula we will be using in our examples for now. The base of the triangle is the side perpendicular to the height of the triangle. The height (or the altitude) of a triangle is a straight line that passes through a vertex (angle) and is perpendicular to the opposite side (called the base). We will now solve a couple of examples in order to show how you can use this formula to calculate the area of any triangle whose height and length of its base are known.
Example 1:
Calculate the surface of this scalene triangle. The length of its base is 9.2 cm and its height is 4.3 cm.
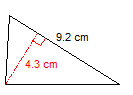
This one is very easy. All you have to do is to place the appropriate values inside our formula and finish the calculation.
T = (9.2 * 4.3)/2
T = 39.56 / 2
T = 19.78 cm2
We can now see that the size of the area is 19.78 cm2. It is extremely important to keep your units in check when calculating areas. If the size of the sides is in meters, the result will be in meters squared (m2).
This assignment was pretty straightforward. Let us try to solve one that is a bit more complicated.
Example 2:
Find the area of this triangle. Its height is 6.7 cm and the length of the opposite side is 4 cm.
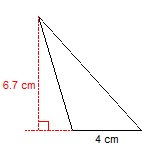
Now, this one is a bit trickier. You can see that the height does not pass through a vertex, but it looks like it forms a larger right triangle with an extended version of what should be the base. Do not let it confuse you. You can still use the formula we used before and the same procedure applies.
T = (6.7 * 4) / 2
T = 26.8 / 2
T = 13.4
You may be asking yourself: “How come?” Well, we will solve it using a more complicated way to show you why this approach still works. First, we will form the equation for calculating the area of the larger right triangle. The height is one leg of the triangle and the extended base is the other. And since two right triangles can form a rectangle, its area is half the area of a rectangle with the legs as its sides.
T1 = (h * (b + x)) / 2
T1 = (6.7 * (4 + x)) / 2
T1 = (26.8 + 6.7 * x) / 2
This is almost as far as we can go with that equation. So now we have to find the area of the smaller right triangle whose legs are the height of the triangle and x (the extension of the base). If we use the same principles as before, the equation for its area (T2) is:
T2 = (6.7 * x) / 2
The only thing left to do now is to subtract the area of the smaller right triangle from the area of the larger right triangle. That should give us the area we are interested in as a result.
T = ((26.8 + 6.7 * x) / 2) – ((6.7 * x) / 2)
T = (26.8 + 6.7 * x – 6.7 * x) / 2
T = 26.8 / 2
T = 13.4
As you can see, the result is the same as before. So do not let an unusual drawing confuse you. If you know the height of a triangle and the length of its base, you can calculate its area using this formula.
This is the basic information you need to have about a triangle. As we progress and put more lessons on this site, we will expand this article with everything you need to know in order to grow your mathematical skills and knowledge.
If you wish to practice everything you learned about triangles here, please feel free to use the math worksheets below.
Triangles exams for teachers
| Exam Name | File Size | Downloads | Upload date |
|
Classification – Sides
|
|||
| Triangles – Classification – Sides – easy | 624.3 kB | 4509 | September 3, 2019 |
| Triangles – Classification – Sides – medium | 595.8 kB | 3995 | September 3, 2019 |
| Triangles – Classification – Sides – hard | 454.1 kB | 3697 | September 3, 2019 |
|
Classification – Angles
|
|||
| Triangles – Classification – Angles – easy | 621.2 kB | 3837 | September 3, 2019 |
| Triangles – Classification – Angles – medium | 610.9 kB | 3206 | September 3, 2019 |
| Triangles – Classification – Angles – hard | 454.6 kB | 3296 | September 3, 2019 |
|
Classification – Sides and angles
|
|||
| Triangles – Classification – Sides and angles – easy | 613.8 kB | 4093 | September 3, 2019 |
| Triangles – Classification – Sides and angles – medium | 610.2 kB | 3423 | September 3, 2019 |
| Triangles – Classification – Sides and angles – hard | 454.2 kB | 3209 | September 3, 2019 |
| Triangles – Finding angles | 528.5 kB | 5855 | September 3, 2019 |
| Triangles – Equations – Angles | 541.1 kB | 3982 | September 3, 2019 |
|
Triangles – Area
|
|||
| Triangles – Area – very easy | 659.3 kB | 2984 | September 3, 2019 |
| Triangles – Area – easy | 638.7 kB | 3295 | September 3, 2019 |
| Triangles – Area – medium | 653.3 kB | 3493 | September 3, 2019 |
| Triangles – Area – hard | 647.2 kB | 3088 | September 3, 2019 |
Triangles worksheets for students
| Worksheet Name | File Size | Downloads | Upload date |
| Triangles – Classification | 6.8 MB | 4236 | September 3, 2019 |
| Triangles – Find the missing angle | 6.9 MB | 7623 | September 3, 2019 |
| Triangles – Area | 6 MB | 4590 | September 3, 2019 |